Разработка задач для проверки знаний и умений учеников в соответствии с требованиями проекта стандарта 2010 года по теме «Функции»

а) б)

Данная задача аналогична задаче №7 из отметки «3». Усложнение происходит из за того, что идет работа с двумя более сложными функциями.

Существуют ли значения аргумента, при которых:

а) функция принимает значение, равное 5;

б) функция принимает значение, равное –4.

Задача аналогична №2 из отметки «3», здесь рассматривается более сложная функция, возможно получение различных ответов.

Найдите область определения каждой из функций:

а) ; б);в) ;

г) д) е) .

Задача аналогична №3 из отметки «3», заданы более сложные функции.

Пусть Найдите:

а) в)

б) г)

Докажите, что график функции:

а) целиком расположен в верхней полуплоскости;

б) не пересекает ось x;

в) не пересекает ось y.

Задача имеет нестандартную запись условия, но имеет достаточно простое решение.

Отметка «5»

Ученик должен решать задания отметки «3» и «4». Для получения отметки «5» необходимо уметь решать задачи на применение знаний (умений) в незнакомой ситуации, для решения нового круга задач, использовать творческий перенос знаний (самостоятельное использование ранее усвоенных знаний в новой ситуации, для решения проблемы; видение проблемы и способов ее решения и т.п.), ученик должен решать задачи среднего и сложного уровня имеющие нестандартный вид, должен уметь решать задачи на применение не только математического аппарата, но и логического, физического и др.

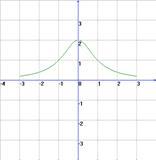
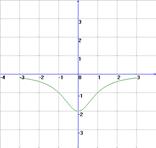
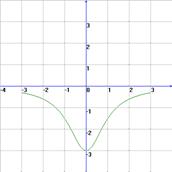
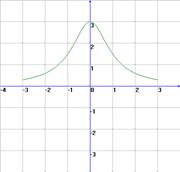
Графические: 1) На рисунке изображены графики функций

; ; ; .

Для каждого графика укажите соответствующую формулу.

Тонкости педагогики:

Формирование нравственной культуры старшеклассников с учётом возрастных особенностей
Процесс нравственного развития старших школьников носит личностно обусловленный характер. Не случайно ведущие исследователи содержания школьного воспитания указывают на необходимость учёта возрастных и индивидуальных особенностей учащихся, способствующих или, наоборот, негативно влияющих на формиро ...

Урок – основная форма организации обучения в школе
Я считаю, что примером применения преподавания является урок. Что такое урок? Ответ на данный вопрос весьма затруднителен на сегодняшний день. До настоящего времени в педагогической науке преобладающем является мнение, согласно которому урок – это систематически применяемая для решения задач обучен ...

Экспериментальное исследование воображения детей старшего дошкольного возраста
В исследовании принимали участие дети старшего дошкольного возраста МОУ ДО "Центр развития ребенка - д/с №345", общеразвивающего вида. Количество испытуемых 30 человек, по 15 человек из экспериментальной и контрольной групп. Целью констатирующего эксперимента было выявление уровня развити ...