Различные методические подходы к формированию табличных навыков сложения и вычитания с точки зрения возможностей непроизвольной памяти

Дети: На доске осталось 10 палочек. Из 13 вычесть 3 – получится 10.

Учитель: Мы закончили решение задачи? Нет! Нам надо отдать Вите всего 4 палочки. Мы же ему отдали 3 палочки. Сколько палочек еще надо отдать ему?

Дети: Еще надо отдать 1 палочку. Из 10 вычесть 1 – получится 9.

Учитель: Теперь повторите еще раз задачу и скажите полностью ответ.

Дети: Из 13 палочек вычесть 4 палочки – получится 9 палочек. На доске записывается рядом два вида примеров:

9+4=13, 13-4=9.

Как видно из изложенного, сначала сопоставляются два примера: на сложение и на вычитание (из суммы второго слагаемого). Затем решаются теми же рассуждениями другие пары примеров: 9+5=14, 14-5=9 и т.д.

При таком противопоставлении двух примеров постоянными для пары остаются числа, над которыми совершаются операции. Так, например, при решении пары примеров 9+4=13 и 13-4=9 логические операции совершаются над шестью числами: 9,4,13,10,3,1. если сопоставить последовательность операций при решении последней пары, то схематически это выглядит так:

9+4= 13-4=

9+1=10, 13-3=10,

(4-1=3) (4-3=1)

10+3=13 10-1=9

Сравнивая отдельные логические операции, мы обнаружим, что при решении двух данных взаимообратных примеров совершается как бы замкнутый цикл операций, следующих одна из другой; тем самым решение двух примеров сливается как бы воедино.

Процесс решения начинается с числа 9 и кончается этим же числом. Сопоставляя попарно эти действия, мы обнаружим, что пары промежуточных действий (9+1=10 и 10-1=9; 4-1=3 и 4-3=1; 10+3=13 и 13-3=10) также соответственно взаимообратные.

В существующей методике при объяснении сложения и вычитания с переходом через десяток принято обычно фиксировать процесс решения кратко, в два этапа:

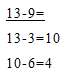
Между тем пропущенный второй этап (9-3=6) наиболее важен, и потому целесообразно записывать решение примера на первых порах в три строки, а потом вообще к устному решению, без письменной фиксации промежуточных результатов, сразу записывая ответ.

Действия сложения и вычитания в пределах 20 входят в таблицу сложения и вычитания однозначных чисел и поэтому должны быть хорошо заучены. При этом надо обратить внимание не на раздельное изучение таблицы сложения и таблицы вычитания, а на заучивание четверок примеров.

В случае равных слагаемых четверка взаимосвязанных примеров вырождается в пару примеров: 6+6=12; 12-6=6.

Если в практике обучения подвергать перестройке во взаимообратные не только примеры на сложение, но и примеры на вычитание, то ассоциации всегда "6 да 9-15", "15 без 9-6" проявляются быстро и безошибочно.

Одновременное изучение сложения и вычитания облегчает осуществление процессов контроля (проверки результатов).[23,c.90]

Изучение действий в пределах второго десятка имеет важное значение для дальнейшего изучения математики в начальной школе.

Как известно, письменное и устное сложение и вычитание многозначных чисел основываются, в конечном счете на твердом знании таблицы сложения и вычитания в пределах 20. кроме того, первичное ознакомление с понятием умножения (деления) целесообразно также осуществить в пределах двух десятков, т.е. до изучения всех случаев сложения и вычитания в пределах 100 (до решения примеров вида 67+9, 67+29).

Математика начальных классов опирается на четыре действия: сложение, вычитание, умножение и деление. Благодаря своевременному внедрению четырех действий мышления обогащается познанием аддитивных свойств числа (разложимости целого числа в виде произведения нескольких множителей).[41,c.54]

Представляется естественным воспользоваться при изучении действий в пределах 20 теми навыками, которые были упрочены при обучении методом укрепления в пределах первого десятка.

Противопоставление действий сложения и вычитания создает условия для одновременного изучения соответствующих пар задач, например, на увеличение уменьшение числа на несколько единиц.

"Сложение и вычитание в пределах второго десятка" изучается по трем следующим разделам:

1. Нумерация и простейшие случаи сложения и вычитания в пределах 20, когда в составе соответствующих примеров обязательно встречается число 10, например: 10+7, 17-7, 7+10, 17-10.

2. Сложение и вычитание без перехода через десяток (15+3, 3+15, 18-3, 18-15).

3. Сложение и вычитание с переходом через десяток (9+7, 16+9).

Изучение темы "Сложение и вычитание в пределах 20 без перехода через десяток" целесообразно построить также на основе противопоставления взаимообратных примеров на сложение и вычитание.

Учитель: (Ставит на полку слева 1 пучок, изображающий десяток, и справа 3 палочки) Сколько палочек отложено?

Тонкости педагогики:

Перспективы развития дошкольного образования в России
Основными документами, задающими целевые ориентиры государственной образовательной политики, являются Концепция модернизации российского образования, Приоритетные направления развития образовательной системы Российской Федерации до 2010 года. Необходимая предпосылка общедоступности качественного об ...

Природа как средство развития словаря детей дошкольного возраста
Развитие словаря дошкольников - актуальная проблема методики развития речи. Содержание словарной работы в дошкольном учреждении определяется программой развития и воспитания детей. Одним из путей ее решения нам представляется ознакомление с природой, формирование у детей эмоциональной отзывчивости ...

Классификация алалии
Алалия - явление неоднородное и по своим механизмам и по своим проявлениям и по степени выраженности речевого недоразвития. Поэтому при составлении классификаций алалии используют разные критерии и разные подходы к ее изучению. (см [1]) Так А. Либман (1925) по патогенетическому принципу выделил 4 ф ...