Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа

6) Периодичность.

Изучению этого свойства необходимо уделить особое внимание, так как учащиеся впервые сталкиваются с периодическими функциями. Для отработки понятия периодичности функции целесообразно использовать следующие упражнения.

1. На рисунке изображена часть графика периодической функции на отрезке [-2;2], длина которого равна периоду функции. Постройте график функции на отрезках [-6;-2], [2;3].

2. Постройте график периодической функции y=f(x), с периодом равным 2, если известно, что f(x)=х2/2 на отрезке [-1;1].

3. Является ли число 16p периодом функции y=sin x? А ее основным периодом?

4. Найти основные периоды функций y=sin(6x), y=соs(x/2), y=sin(кx).

5. Докажите, что если функция y=f(x) является периодической, то и y=k*f(x)+b тоже периодическая.

6. Пусть функция f периодическая, Т1 и Т2 – ее периоды. Докажите, что любое число вида nТ1 +mТ2, где n,mÎN, также является периодом функции f.

7. Докажите, что функции f(x) = sin x2 и cos (x)*cos Öx не являются периодическими.

8. Докажите, что возрастающая функция не может быть периодической. И т.п.

Следует обратить внимание учащихся на тот факт, что периодическая функция имеет бесконечное множество периодов, среди которых стараются выделить, если это возможно, наименьший положительный период, который называют основным.

После этого все свойства тригонометрических функций желательно проиллюстрировать на графике и свести в одну таблицу.

Для дальнейшей отработки навыков по исследованию тригонометрических функций и построению их графиков используют гармонические колебания, которые имеют вид y =Asin(wt+a) и y =Acos(wt+a). Основной целью введения гармонических колебаний является наглядная демонстрация того, как изменяются свойства функций в зависимости от значения коэффициентов A,w и a. При этом целесообразно использовать задания вида:

1.По графику функций определите задающую ее формулу:

Рис.6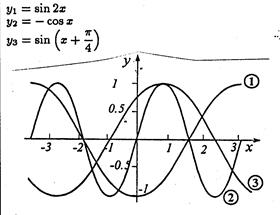

2. Какими свойствами обладают данные функции на отрезке [-p/2; p/2], а на отрезке [0; p]?

Какими свойствами обладают данные функции на данных промежутках?

Тонкости педагогики:

Психологические основы непроизвольной памяти младших школьников
Развитие передовой философской общественной и естественнонаучной мысли оказывало свое положительное влияние на разработку специальных вопросов психологической науки, в том числе и вопросов психологии памяти. В связи с этим в развитии отечественной и зарубежной психологии были не только общие черты, ...

Особенности образовательного процесса в кадетской школе
Образовательный процесс - это целенаправленный и организованный процесс получения знаний, умений, навыков в соответствии с целями и задачами образования, развития личности [сл. Полонский, ст.64]. Кадетская школа - интернат - вид государственного бюджетного образовательного учреждения, реализующего ...

Составление проектов физкультурных праздников для детей старшего дошкольного возраста
Проект «Приобщение дошкольников к истокам национальной культуры через физкультурные праздники» Актуальность темы проекта Необходимость приобщения молодого поколения к национальной культуре трактуется народной мудростью: наше сегодня, как никогда наше прошлое, также творит традиции будущего. Наши де ...