Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа

Больше всего проблем, связанных с неоднозначностью соответствия между точками и числами на окружности возникает при решении задач вида: «Найти на числовой окружности точки с ординатой (абсциссой) большей Ö3/2 и записать, каким числам они соответствуют».

Такие неравенства, характеризующие дугу, рекомендуется на начальном этапе составлять в два шага. На первом шаге составить так называемое «ядро» аналитической записи p/3 < t < 2p/3, и только на втором составить общую запись p/3+2pk < t < 2p/3+2pk, где к Î Z.

По этому поводу осмелюсь не согласиться с статьей [10], в который автор пишет, что уточнение «где к Î Z» можно опускать, записывая его только в парадных случаях – на контрольных или экзаменационных работах. В большинстве случаев это действительно можно делать совершенно безболезненно, но как быть, если при отборе корней уравнения или неравенства, или при наложении определенных ограничений на функцию, параметр к сможет принимать не все а, например, только положительные или только четные значения?

Учащиеся, привыкшие писать +2pk, не задумываясь над тем, какие значения может принимать параметр к, и в этом случае напишут +2pk, что автоматически сделает их решение неверным.

Это приведет и к недопониманию того факта, что, например, множества «4pk, где к Î Z» и «2pk, где к Î 2Z» совпадают. Это, в свою очередь, может породить затруднения при рассмотрении функций с периодом, равным 4p. А ведь таким функциям уделяется немало времени при изучении темы «Тригонометрические функции».

Таким образом, нельзя оставлять недоработанными никакие, даже самые маленькие детали, ведь незначительные с виду недоработки, возникающие при изучении числовой окружности, в процессе изучения самих тригонометрических функций могут стать причиной возникновения больших пробелов в знаниях.

Теперь, когда мы научились работать с числовой окружностью как самостоятельным объектом, можно приступать к введению самих тригонометрических функций.

Не стоит забывать, что определения тригонометрических функций с помощью числовой окружности плохо укладываются в сознании ребят по одной простой причине: на первом этапе определения были даны в геометрической трактовке – как отношения сторон прямоугольного треугольника.

Из психологии известно: «если какое-нибудь важное понятие вводится в первый раз, то ассоциации, сопутствующие ему, врезаются в сознание учащегося чрезвычайно прочно. Последующие впечатления бывают слабее и не могут стереть того обличия, в котором это понятие явилось впервые». [5]

Несмотря на то, что мы уже использовали окружность для введения «новых» определений синуса и косинуса на этапе расширения множества значений, принимаемых углом необходимо еще раз провести взаимосвязь между прямоугольным треугольником и числовой окружностью.

Напомним, что в школьных учебниках этому факту почему-то не уделяется должного внимания (см. главу «Анализ изложения темы «Тригонометрические функции» в различных школьных учебниках»), поэтому учителю стоит обратить внимание на то, чтобы при введении тригонометрических функций на этом этапе были озвучены следующие моменты.

Рассмотрим числовую окружность единичного радиуса, расположенную в прямоугольно декартовых координатах. Рис.1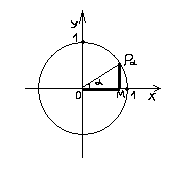

В положительном направлении от оси ОХ отложим угол a такой, что 0 < a < 900. Обозначим полученную на окружности точку как Рa. Опустим из точки Рa перпендикуляр на ось ОХ, получим точку М. Рассмотрим получившийся прямоугольный треугольник ОМРa. Sina по определению равен отношению МРa/ОРa, но радиус окружности ОРa равен единице, следовательно, Sina = МРa. Аналогичным образом, cosa = ОМ. Заметим, что длина ОМ - это абсцисса точки Рa в прямоугольно-декартовой системе координат, а длина МРa - ее ордината. Таким образом, синус и косинус угла a определяются через ординату и абсциссу точки Рa, что является более удобным при работе в прямоугольно-декартовой системе координат.

Работая с числовой окружностью, мы уже усвоили тот факт, что так как длина дуги единичной окружности легко выражается через центральный угол, на нее опирающийся, то точку Рa, можно построить и другим способом - откладывая дугу заданной длины. А так как длина дуги – всегда действительное число, значит, от тригонометрических функций углового аргумента легко можно перейти к тригонометрическим функциям числового аргумента.

Сейчас вернемся к наложенным на угол a ограничениям. Угол a принадлежит промежутку от 00 до 900, а значит и длина дуги лежит между нулем и p/2. Используя все ту же геометрическую интерпретацию, легко показать, что эти определения можно распространить и на любые углы и числа.

Понятия тангенса и котангенса можно вводить двояко: как отношение синуса к косинусу (косинуса к синусу) и как ординату (абсциссу) точки пересечения касательной к окружности в точке (1;0) ((0;1)) и прямой ОРa.

Рис.2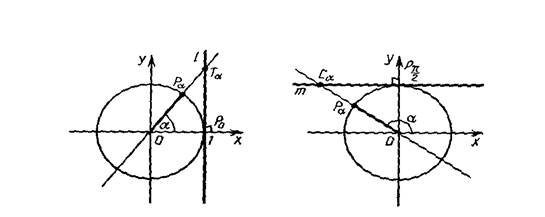

Тонкости педагогики:

Выпуск специалистов
На сегодняшний день в США большую часть взрослых студентов составляют женщины. В данный момент они представляют 41 % ученых в области наук о жизни, 23% химиков, 18% геологов, 30% математиков – специалистов в области вычислительной техники, 6% инженеров и 57% психологов. Для женщин существуют специа ...

Краткий исторический обзор подходов к изучению обыкновенных дробей в Российской школе
Методика преподавания обыкновенных дробей развивалась параллельно с методикой преподавания целых чисел. Подходы к изучению целых чисел использовались и при изучении дробей. В начале XIX века немецкий педагог А.В. Грубе (последователь И.Г. Песталоцци) предложил методическую систему, известную как «м ...

Анализ учебно-программной документации
Специальность 030500.06-Профессиональное обучение (информатика, вычислительная техника, компьютерные технологии) специализации 030501.06 Дисциплина «Компьютерные Коммуникации и Сети»: изучается на 3 курсе в 5 и 6 семестре; зачет в 5 семестре, в 6 семестре – курсовая работа и экзамен; на дисциплину ...