Методическая схема изучения признаков равенства треугольников

2. На основании полученного рисунка сформулируйте теорему записать ее условие и заключение;

3. Сообщить идею доказательства;

4. Сообщить план доказательства;

5. Провести доказательство с четким выделением его шагов;

6. Осуществить закрепление его доказательства;

7. Рассмотреть с учащимися задачи на примере признака.

Итак, пусть по сторонам В, С и углу А с помощью транспортира и линейки построено два треугольника: ∆ АВС и ∆ А1В1С1

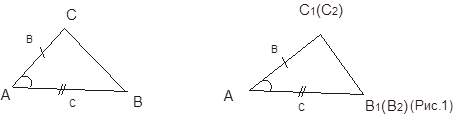Что можно сказать о ∆ АВС и ∆ А1В1С1 ?

После о том, что эти треугольники равны, формулируем теорему. Выясняем: что дано в этой теореме, а что надо доказать. Рядом с рисунком 1 краткую запись теоремы:

Дано: АВ =А1В1; АС=А1С1; А = А1

Доказать: ∆ АВС = ∆ А1В1С1

Сообщаем ученикам идею доказательства: рассмотреть третий ∆ А1В2С2, который: 1. равен ∆ АВС и расположен таким образом, что 2. его вершина В2 лежит на полупрямой А1В1; 3. вершина С2 находится в той же полуплоскости относительно прямой А1В1, в которой лежит вершина С1.

Теорема будет доказана, если установлено, что ∆ А1В2С2 совпадает с ∆ А1В1С1.

Составляем план доказательства:

1. Рассмотрим ∆ А1В2С2, о котором говорилось выше;

2. Докажем, что вершина В2 совпадает с вершиной В1;

3. Докажем, что луч А1С2 совпадает с лучом А1С1;

4. Докажем, что вершина С2 совпадает с вершиной С1;

5. Сделаем заключение о равенстве ∆ АВС и ∆ А1В1С1.

Приводим краткую запись доказательства на доске (оно выполняется учителем по ходу изложения, записывать доказательство в тетрадях не нужно),

1) ∆ А1В2С2 = ∆ АВС аксиома IV3

2) т.к. А1В1 = А1В2, то В2 совпадает с В1 аксиома IV1

3) т.к. В1А1С1 = В2А1С2, то лучи А1С2 и А1С1 совпадают

аксиома IV2

4) т.к. А1С1 = А1С2, то точки С2 и С1 совпадают аксиома IV1

5) ∆ А1В2С2 и ∆ А1В1С1 совпадают п.п. 2,4

6) ∆ АВС = ∆ А1В1С1 п.п. 5,1

Вопросы для закрепления

1. Как был выбран ∆ А1В2С2?

2. Почему вершина В2 совпадает с вершиной В1 ?

3. Зачем нужно доказывать совпадения лучей А1С2 и А1С1 ?

4. Почему вершина С2 совпадает с вершиной С1 ?

5. Почему делается вывод о равенстве ∆ АВС и ∆ А1В1С1

Рассмотрим еще одну методическую схему изучения этого признака:

1. рассмотреть решение ряда подготовительных задач;

2. доказать первый признак рав-ва треугольников.

Подготовительные задачи:

1) отрезки А1В1 и А1В2 равны отрезку АВ и отложены на полупрямой А1В1. Что ещё можно сказать о расположении отрезков А1В1 и А1В2 ?

2) Углы В1А1С1 и В1А1С2 равны углу А. Что можно сказать о расположении углов В1А1С1 и В1А1С2 ? Что можно сказать о расположении лучей А1С1 и А1С2, если они находятся в одной полуплоскости относительно прямой А1В1?

3) Треугольники А1В1С1 и А1В2С2 равны, вершина В2 лежит на полупрямой А1В1, вершина С2 лежит в одной полуплоскости (относительно прямой А1В1) с вершиной С1. Докажите, что эти треугольники совпадают, т.1. вершина В2 совпадают с вершиной В1, вершина С2 – с вершиной С1.

Рассмотренная первой методическая схема доказательства основана на применении репродуктивного метода обучения и он наиболее эффективен при изучении третьего признака равенства треугольников, наиболее сложного.

Тонкости педагогики:

Университетские реформы второй половины XIX века
В ходе проводившихся в России в 60-е гг. преобразований проблемы развития университетов занимали не последнее место. Реформы Александра II нуждались в резком увеличении числа образованных людей, серьезных переменах в сфере народного просвещения. Не случайно, поэтому стал вопрос о существенных измен ...

Авторитет родителей и его влияние на развитие личности ребенка
Авторитет – одно из важных условий семейного воспитания. Семья оказывает влияние на формирующуюся личность ребенка, не только целенаправленным воздействием взрослых ее членов, но и всем образом жизни. Отношения в семейном коллективе требуют взаимопонимания, ответственности, умение организовать отно ...

Основы здорового образа жизни. Физическая культура в обеспечении здоровья
Охрана собственного здоровья – это непосредственная обязанность каждого, он не вправе перекладывать ее на окружающих. Ведь нередко бывает и так, что человек неправильным образом жизни, вредными привычками, гиподинамией и перееданием уже к 20-30ти годам доводит себя до катастрофического состояния, и ...